Measuring Muzzle Velocity Standard Deviation - Are we doing it right?

[Kent Goldings]

I was watching a Youtube video where the OP was doing some load testing. He fired several 5-round groups while measuring the muzzle velocity, computed the mean and standard deviation of that random variable.

He presented the results proudly and was moving to make a conclusion about each different loading. That's when I began to question his method.

My thinking was that the margin-of-error on the standard deviation of the muzzle velocity gathered from only 5 rounds was too large to make such judgements.

In order to support my think, I did some load testing of my own. Using CCI Standard velocity 22 LR, I chronographed an entire 50-round box.



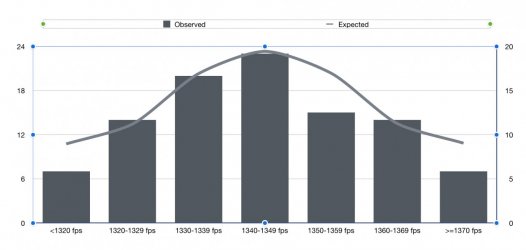
I compared the distribution of the observed velocities with what would be expected, if the muzzle velocities obeyed a normal distribution.



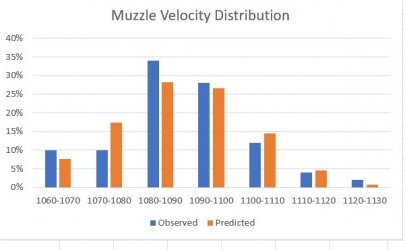
After performing a "goodness-of-fit" statistical comparison of the two distributions, I found that the two did not differ in a statistically significant way. That is, the observed distribution supports the claim that muzzle velocities are distributed normally.

If this is the case, a sample size of 5 does not provide conclusive information on the standard deviation of the muzzle velocity.

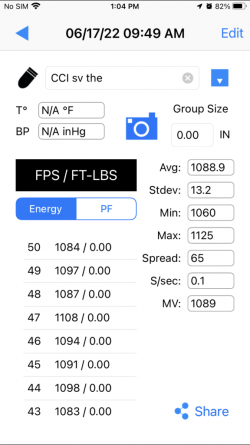
For example, the standard deviation of the 50 shots above was 13.1 fps.

If that computation had been done after only five rounds, the 95%-confidence interval that estimates the standard deviation of the entire box ranges from 8 to 40 fps. That is, the standard deviation of the box could be as high as 40 fps.

 

[Beerman]

Nice work, good data presentation. Now show the Coefficient of Variation for that data set and you’ll have even more meaningful info.

 

[Kent Goldings]

Nice work, good data presentation. Now show the Coefficient of Variation for that data set and you’ll have even more meaningful info.

I actually used a chi^2 goodness-of-fit test. If anyone is curious, they can look it up on YouTube.

I didn’t want to make a math lecture. I just wanted evidence to support that muzzle velocities are normally distributed.

That makes computing the confidence-interval estimating the standard deviation actually valid.

 

[Jezman]

Does it really matter? If you can hit your intended target any time at your rifles range. Are those numbers really that important?

 

[meketrefe]

Standard deviations are not Good or Bad, only indicators of how spread out ones data is. So It depends if one expects the distribution to be centered or spread out around the mean.

The sampling scheme is key and considering the many other variables that can change from start to finish.

That is why many manufactures test batches in a lab.

Once you get to a point there is little value in investing huge amounts of time investigating alternative methods. I mean from the practical point of view. From the entertainment or academic point of view that is a different story.

 

[Kent Goldings]

Does it really matter? If you can hit your intended target any time at your rifles range. Are those numbers really that important?

It matters because the loader was making decisions based on these numbers.

Accuracy in a load is a product of consistency. That required measuring.

Manufacturers can do extensive testing to make their loads consistent.

People that load their own don’t have that luxury. I ran this test with 22LR because I didn’t want to waste components doing with a centerfire caliber.

 

[dsdmmat]

The difference is you are shooting a commercial product which has a 100,000 to 100,000,000 rounds in a lot. So statistically your Bach of 50 shots is less significant than most handloaders who fire 5 rounds to develop a load where they are going to make less than 1000 rounds.

A can of powder will only load so many rounds, so each lot must be checked for Velocity and Standard Deviation with the opening of a new can of powder.

If you hand loaded 5 cartridges and shot 5 cartridges you have the standard deviation of 100% of your load. Which is enough for most hand loaders when you think about it. If you get 100 rounds per pound you have a reference for 5% of your lot. A whole lot more than any commercial load will ever have.

Besides Most people don’t shoot enough to care about large batches of data. They shoot 3 or 5 groups and are happy enough with the results.

 

[Kent Goldings]

You have to shoot thousands of rounds of ammunition. The chi-square test factors in the sample size. As long a you shoot 30 or more, the central limit theorem kicks in.

 

[kev74]

Its been almost 20 years since I sat in a statistics class and I don't miss it.

If your goal is to get a rough idea about a load's (or a loading process') consistency based on something more concrete than a hunch or intuition, smaller batches are fine.

If, on the other hand, you want to get more statistically significant data, you need a larger sample size.

The guy who chronos 5 rounds is getting better data than the guy who relies solely on perceived recoil or holes in a target.

There's no right answer, just how far down the rabbit hole you might want to go.

 

[repete]

STOP!! you're giving me a headache!

 

[Acer-m14]

all i know what ever 22LR i feed this .. the wood chuck is dead ..

 

[spat]

Does it really matter? If you can hit your intended target any time at your rifles range. Are those numbers really that important?

The basic explanation is that the standard deviation tells you how consistent the velocity is in that batch of ammo.

If the number is large, then your muzzle velocity will be inconsistent.

OP was saying basically than 5 rounds isn't enough to know if your ammo is good or not.

5 rounds with only a 5fps variation could be very good ammo, or it could have been a lucky string. You just can't tell after 5 rounds.

100 rounds with a 10 fps variation would be much much better.

The rest was a discussion about the math that proves it.

 

[Beerman]

all i know what ever 22LR i feed this .. the wood chuck is dead ..

View attachment 162798



View attachment 162799

My father bought a 142 with the T handle, like in your pic. I think Mossberg only made the T handle for a year or so before moving to a ball. It still sends groups of 1/2” with ease. It belongs to one of my brothers now, and it gets out regularly.

 

[meketrefe]

The basic explanation is that the standard deviation tells you how consistent the velocity is in that batch of ammo.

If the number is large, then your muzzle velocity will be inconsistent.

OP was saying basically than 5 rounds isn't enough to know if your ammo is good or not.

5 rounds with only a 5fps variation could be very good ammo, or it could have been a lucky string. You just can't tell after 5 rounds.

100 rounds with a 10 fps variation would be much much better.

The rest was a discussion about the math that proves it.

If ones coefficient of variation is low ( below 1) then large sample size is not necessary to see if one spreads are centered around the mean. If the CV is high one should question the whole thing anyway.

3 or 4 strings of 5 rounds (1box) is more than plenty to tell you if you are in the expected range. Then with a low coefficient of variation one can move to the sample size that is representative of the actual use scenario. You should not shoot more or faster than what is required by the use otherwise the variables one may introduce are not a realistic test case.

A high value of Standard Deviation will make the minimum detectable effect increase but one might be inducing wider spread by increasing the size unless it is done in a lab measuring temperatures, and all other conditions. You'll need a larger sample size if you want to find small statistically significant differences but only if you can assure consistent test conditions that is more difficult out of a lab with ammunition. Realistically not needed in this world.

So in sniper and long range school we use the 5 shot spreads to verify the speed spreads and might jump to 5 to 10 strings to test accuracy, consistency and repeatability.

Bench rest folks and catters might have 1000 opinions about sampling and better methods but in the end and in practical terms we use the standard method that has worked so well for generations. On top of that we have doppler now.

If there was a significantly better method snipers and elite shooters will use it but they dont. You buy quality match ammo or reload a clone and you shoot.

I look back and reflect on the many things I did that didnt need to be done but I guess everyone can easily find a reason to spend more time reloading and at the range.

 

[Kent Goldings]

My issue is the nature of sampling a random variable. This is not a problem that can be circumvented through technology or methodology. There is a theoretical limit to the information the Math provides.

I ran 100 mini mags through my 10/22 and the result supports the notion that muzzle velocities are normally distributed.



Any random variable with a normal distribution suffers from sample variation. Any sample-mean and sample-standard deviation are also random variables. The distributions of these are predicable and you can calculate how well a given sample statistic estimates a corresponding parameter.

I’m not suggesting that anybody is doing things incorrectly. Shooters have to use the best estimates for any parameter that is available.